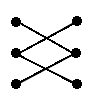
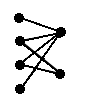
Bipartite graphs and partitions

In a bipartite graph, it is possible to partition the set of vertices into two sets such that none of the vertices in either set are adjacent to one another.

Here are some examples:

In a tripartite graph, the vertices are partitioned into three sets (partitions) so that no two vertices contained in any one partition are adjacent.

An n-partite graph is defined similarly, with the vertices partitioned into n sets or partitions.

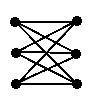
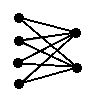
A complete n-partite graph is a graph where every vertex in each partition is connected to all the vertices of the graph which are not contained in that partition A complete n- partite graph is denoted K(p₁, p₂, . . . , p_n) where p_n denotes the number of vertices in each partition. Thus K(3, 3) is a complete bipartite graph with 3 vertices in each partition and K(3, 4, 5) is a complete tripartite graph with partitions of 3, 4, and 5 vertices.

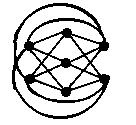K(3, 3)	K(4, 2)	K(2, 3, 2)

Copyright © 1999-2000 SciMathMN