Proof that cylindrical sections have constant sum property

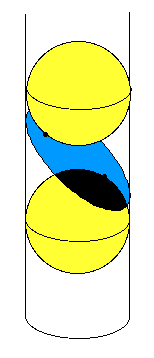
For this proof we assume that an ellipse is a figure satisfying the cylindrical section property. We prove that every such figure satisfies the constant sum property. Elsewhere we give a virtually identical proof for conic sections using more notation.

In the cylinder we can inscribe many spheres, above or below or passing through the plane of the ellipse. Imagine two of these inscribed spheres, one above the ellipse and tangent to it, and one below and tangent to the ellipse. We shall show that the points of tangency are the foci of the ellipse.

Each of these inscribed spheres is tangent to the cylinder in a circle. The distance between those circles, measured along any generating line of the cylinder, is constant. We shall show that the constant distance between those circles is the constant sum of distances from the foci to any point on the ellipse.

Take any point P on the ellipse, and imagine the generating line of the cylinder that passes through P. Along that line there are line segments from P to each of the circles of tangency. These line segments are tangent to the inscribed spheres. Therefore they are the same lengths as any other line segments from P to points of tangency on the spheres. In particular, they are the same lengths as the line segments from P to the points of tangency of the spheres to the plane of the ellipse.

So the sum of the distances from P to the points of tangency of the spheres to the ellipse equals the constant distance between the circles.

In the case of a circle, the two spheres will both touch in the center, so both foci are really one point, the center of the circle. The sum of distances of a point on a circle to the two foci is really two lengths of a radius, which for a circle is constant.