Proof 3 of rectangular coordinate equation

We assume that an ellipse is a figure satisfying the constant ratio property. That is, the ratio of the distances from each point to the focus F and directrix D is the constant e, the eccentricity.

Let d be the distance from F to the line D. Let us put the x-axis perpendicular to D and passing through F. Locate the origin at F.

Without loss of generality, let's assume that the line D is on the positive side of the origin, so that its equation is x = d.

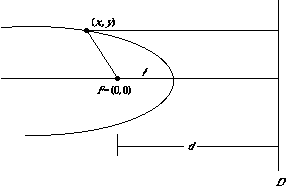
Now suppose (x , y ) is any point on the ellipse. Then the square of the distance from (x , y ) to F is

x ² + y ²,

and the square of the distance from (x , y ) to D is

(d – x )². The constant ratio property says that the ratio of these squares of these distances is the square of the constant e. That is,

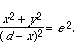
Now on the x-axis there's a point A whose ratio of distances from F and D satisfies the same ratio. Let's say that A is a distance f from F. Then the distance from A to D is d - f, and e ² is also

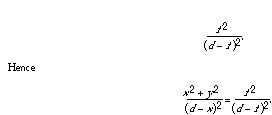
Multiplying both sides to clear the denominator gives

(x ² + y ²)(d – f )² = f ²(d – x )². We're interested in the coefficients for x and and y, so we solve: (d – f )²x ² + (d – f )² y ² = f ²d ² – 2df ² x + f ²x ².

[(d – f )² – f ²] x ² + 2df ² x + (d – f )² y ² = f ²d ².

(d ² – 2df ) x ² + 2df ² x + (d – f )² y ² = f ²d ².

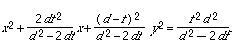
Now we can complete the square on the left to get

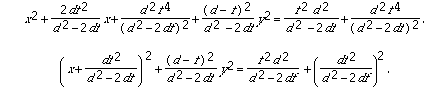
Apparently the equation would be simpler if we shifted the orgin to the left by an amount of

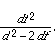
For now, let's just call that amount c. Then the right side is just cd + c ² and the coefficient of y² is

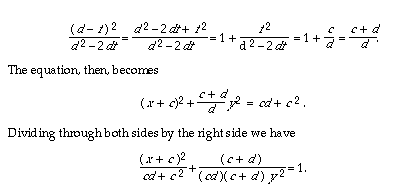
If we rewrite cd as b ² and cd + c ², or b ² + c ², as a ², then our equation is

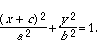
A shift of the origin to the left, or the figure to the right, by a distance c gives us the equation we seek:

<
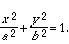